四个自定义 SHAP 图
超越 Python 包,创建 SHAP 值的定制可视化

SHAP 值是了解模型如何进行预测的绝佳工具。SHAP 包提供了许多可视化效果,使这个过程更加简单。话虽如此,我们不必完全依赖这个包。我们可以通过创建自己的 SHAP 图来进一步了解模型的工作原理。在本文中,我们将解释四个定制的 SHAP 图以及您可以从中学到什么。您可以在GitHub1上找到用于创建这些图的代码。
讨论的图表之一是图 1 中的瀑布图。这是一种可视化单个预测的 SHAP 值的好方法。模型做出的每个预测都会有自己的瀑布图。它可以用来准确解释每个特征对最终预测的贡献。例如,这只鲍鱼的壳重量使预测的环数减少了 1.82。
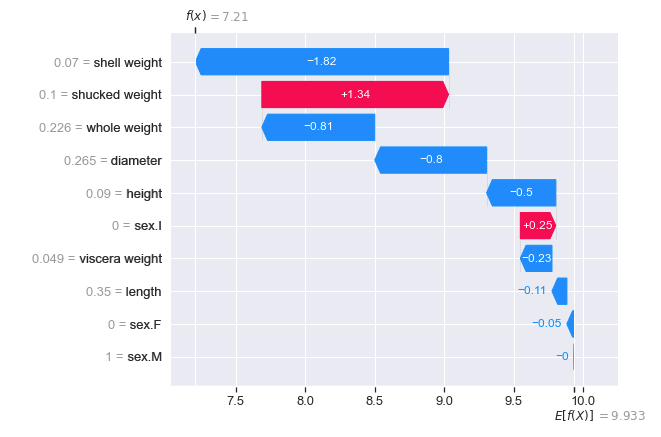
要创建此图,我们首先必须使用 SHAP 包计算 SHAP 值。然后我们将这些值传递到提供的瀑布图函数中。还有许多其他可用的图,但我们不一定非要使用它们。一旦我们有了 SHAP 值,我们就可以自由地创建自己的可视化效果。现在,让我们深入研究第一个。
图 1:SHAP 相关热图
正如我们在瀑布图中看到的,对于给定的预测,模型中的每个特征都会有一个
SHAP 值。我们能够计算这些 SHAP
值在所有预测中的相关性。对每个成对特征组合执行此操作,我们可以构建一个
SHAP 相关性热图,如图 2
所示。在这里我们可以看到,例如,鲍鱼壳直径(diameter)和高度(height)的
SHAP 值的相关性为 0.4。
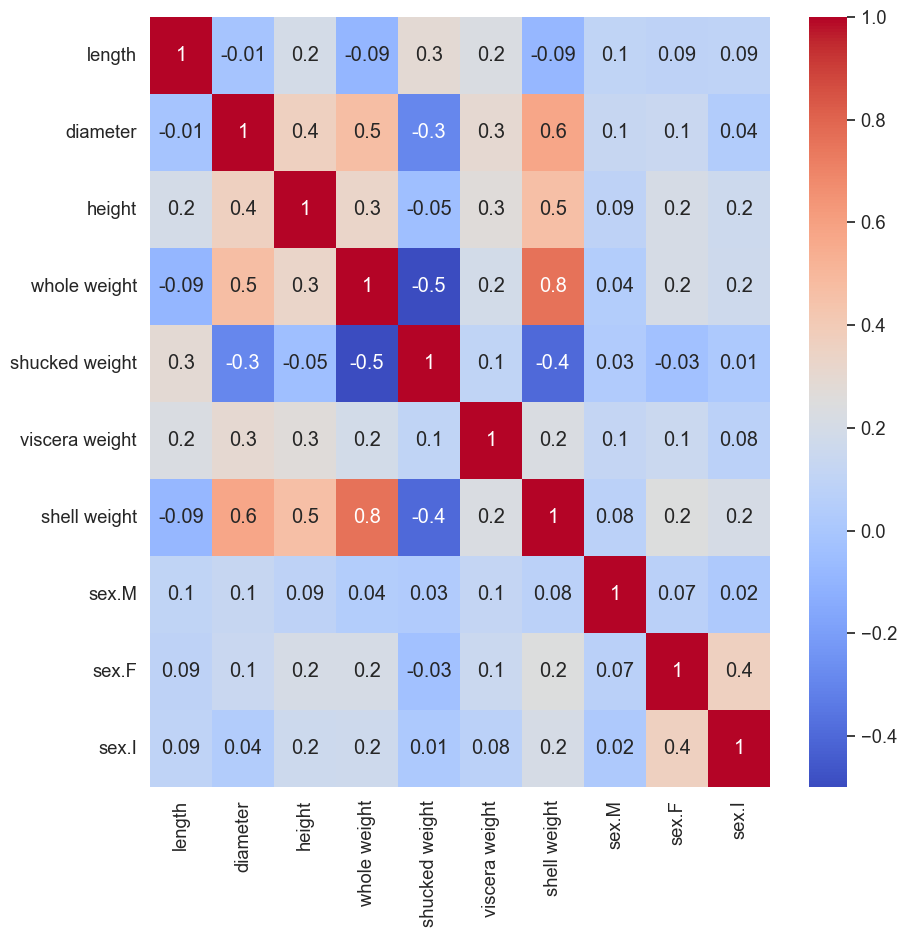
我们可以将其与图 3 所示的标准相关性热图进行比较。这是使用特征值创建的,可以告诉我们特征是否相关。换句话说,它可以告诉我们两个特征是否倾向于朝相同方向或相反方向移动。另一方面,SHAP 值给出了特征对预测的贡献。因此,SHAP 相关性将告诉我们两个特征是否倾向于将预测移向同一方向。
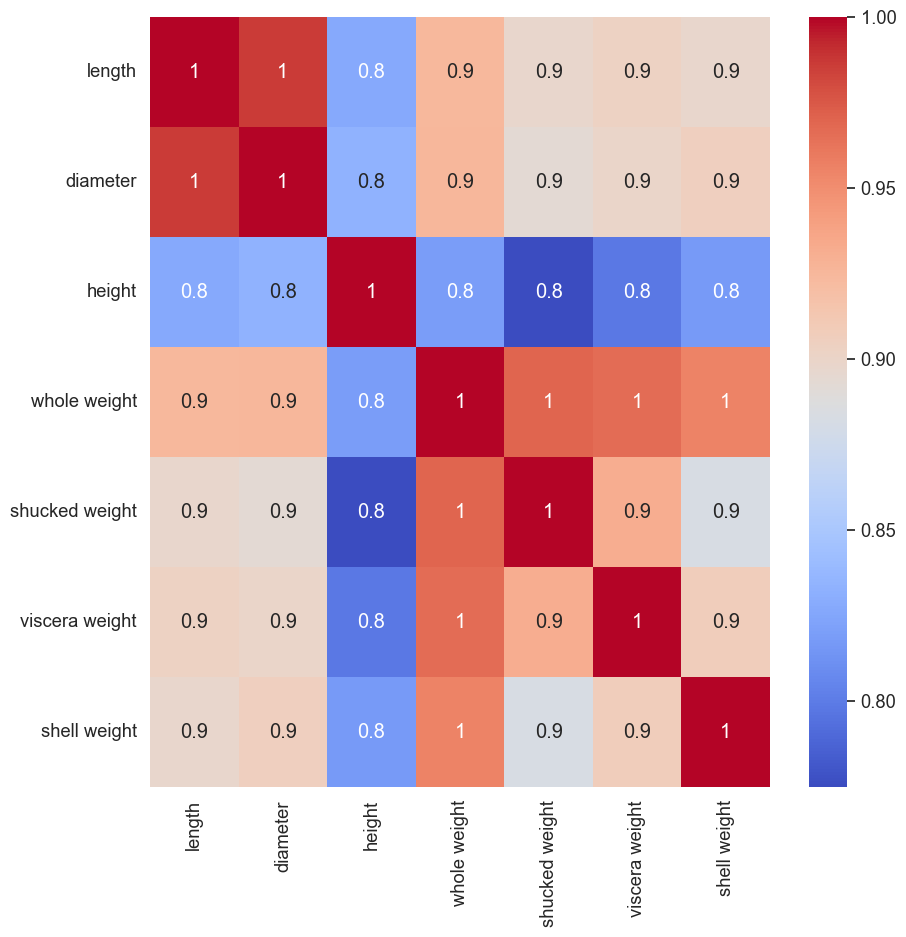
我们已经看到一些差异。请注意,在图 3 中,整重和去壳重呈正相关 (1)。相比之下,这些特征的 SHAP 值呈负相关 (-0.5)。即使这些特征朝同一方向移动,它们的贡献也倾向于将预测朝相反的方向移动。直观地看,这可能看起来很奇怪。一个可能的原因是这两个特征之间存在相互作用。
另一个区别是 SHAP 相关性可以针对连续变量和分类变量进行计算。这是因为无论针对哪个特征计算 SHAP 值,它们始终都是连续的。这就是为什么三个二元变量(即 sex.I、sex.M 和 sex.F)包含在 SHAP 相关性热图中,而不是标准相关性热图中的原因。
图2:调整后的瀑布图
下一个图更像是对现有 SHAP 图的补充。在文章开头的图 1 中,我们查看了瀑布图。我们可以通过添加一些其他信息来了解有关预测的更多信息。查看图 4,我们添加了该鲍鱼的实际环数(即 y=7)。我们还为每个特征添加了分布图。红线表示该特征的平均值。虚线表示用于进行预测的实际特征值。
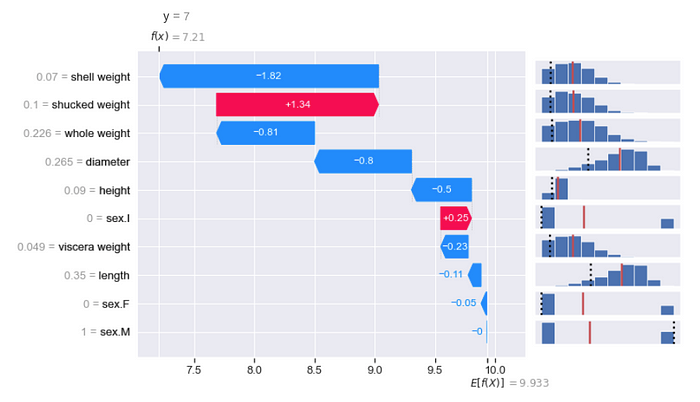
图 5 是可视化此信息的另一种方式。此处,特征被色块包围,其中颜色由特征的值决定。我们坚持 SHAP 包使用的惯例。如果特征的值相对于该特征的平均值较低,则该块将更蓝。如果特征值较高,则该块将为红色。在图 4 中,我们可以看到大多数特征值低于平均值(即红线左侧)。这对应于您在图 5 中看到的所有蓝色块。
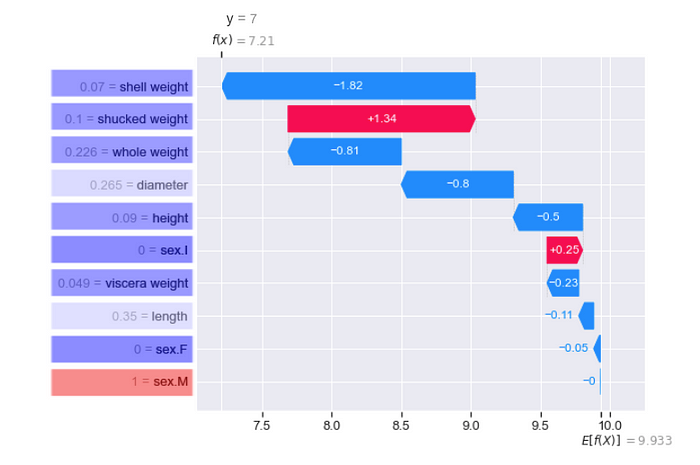
通过在上图中包括实际环数 y,我们能够看到模型对这只鲍鱼的准确度。如果我们发现预测与实际值有很大差异,我们对 SHAP 值的解释可能会改变。在我们的例子中,预测值非常接近实际值。如果它们不同,我们可能会查看瀑布图以了解是否有任何特征导致了错误的预测。
通过添加分布图或色块,我们为特征值提供了背景信息。这使我们能够更全面地解释模型做出该预测的原因。之前我们可以看到哪个因素对预测贡献最大。现在,我们可以开始理解为什么该特征如此重要。为了更好地理解这一点,让我们使用银行业的一个示例。

假设我们建立一个用于接受/拒绝贷款申请的模型。月收入可能是一个重要因素。随着这一特征的下降,您更有可能拖欠贷款。假设该模型拒绝了一项申请。之前我们可以说,“我们拒绝了您的申请,您的月收入是这一决定的主要驱动因素”。现在,通过调整后的瀑布图之一,我们可以说,“我们拒绝了您的申请。这是因为您的月收入远低于我们的平均客户。”
图 3:交互热图
接下来我们将要看的两个图是 SHAP 交互值的可视化。如果您不熟悉这些,我建议您阅读一下分析与 SHAP 的相互作用这篇文章。我们将更深入地介绍如何解释这些值。总而言之,对于给定的预测,我们将有一个 SHAP 交互值矩阵。矩阵的对角线给出主效应,非对角线给出交互效应。每个预测都会有一个这样的矩阵。
为了创建第三个图,我们首先计算所有交互值矩阵中每个单元格的绝对平均值。交互效应减半,因此我们还将对角线外的数值乘以 2。然后我们可以将其显示为热图,如图 6 所示。热图将围绕对角线对称,因此我们仅显示下半部分。
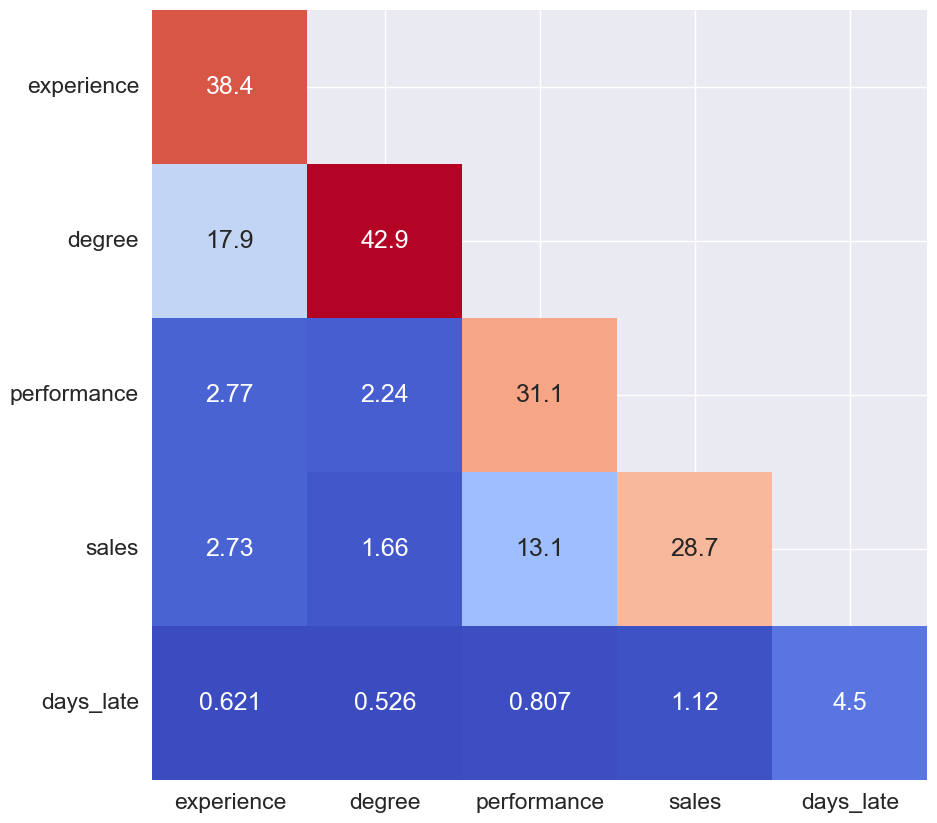
该图与均值 SHAP 图类似,因为它可以突出显示重要特征。但现在,我们可以突出显示重要的主效应和交互效应。例如,我们可以看到经验、学位、绩效和销售额的平均主效应很大。这告诉我们,这些特征往往会对模型的预测产生重大影响。同样,我们可以看到经验.学位和绩效.销售额交互效应很显著。
图 4:交互瀑布图
我们的最后一张图是 SHAP 交互值的瀑布图。这可以以与普通瀑布图相同的方式进行解释。但现在我们无法看到主效应和交互效应如何对预测做出贡献。例如,经验主效应使预测奖金增加了 35.99 美元。同样,经验.程度交互效应使预测奖金增加了 13.76 美元。
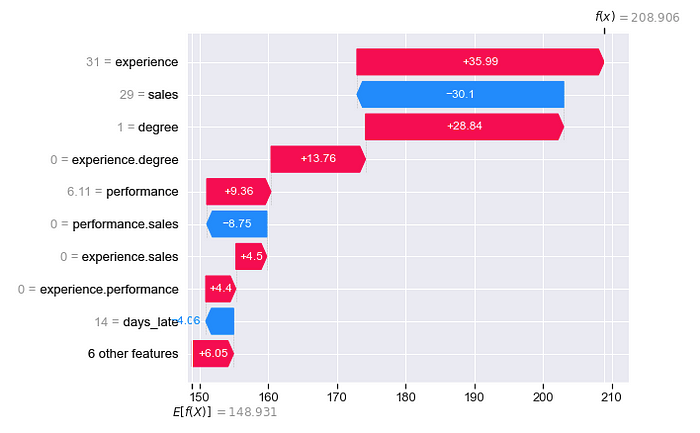
如果您查看用于创建此图的代码,您会发现我们非常狡猾。问题是 SHAP 包没有提供可视化预测交互值的方法。经过一些工作,我们就可以使用为正常 SHAP 值创建瀑布图的函数。如图 8 所示,这涉及将二维矩阵中的交互值转换为一维数组。一旦我们有了这个数组,我们就可以将其传递给瀑布函数,SHAP 会将其视为一组正常的 SHAP 值。

参考
S. Lundberg, SHAP Python package (2021), https://github.com/slundberg/shap
S. Lundberg & S. Lee, A Unified Approach to Interpreting Model Predictions (2017), https://arxiv.org/pdf/1705.07874.pdf
「AI秘籍」系列课程:

Github, https://github.com/hivandu/public_articles/blob/main/src/interpretable_ml/SHAP/shap_custom.ipynb↩︎
四个自定义 SHAP 图
